树
一.树形结构
像数组、栈、队列、默认都是线性结构类型。常见的树形结构有二叉树和多叉树(大于两个叉的树)。
开发中常见的树形结构有: 文件夹目录、DOM结构、路由的配置...... (树的数据结构是非常重要的)
常见概念
节点 (根节点、父节点、字节点、兄弟节点)
子树 (左子树、右子树),子树的个数称之为度
叶子节点 (度为0的节点) 非叶子节点 (度不为0的节点)
节点的深度 (从根节点到当前节点所经过的节点总数)
节点的高度 (从当前节点到最远叶子节点经过的节点总数)
树的层数 (树的高度、树的深度)
有序树( 节点按照顺序排列)、无序树
二.二叉树
二叉树是每个结点最多有两个子树的树结构 ,每个节点的度最多为2。 通常子树被称作“左子树”(left subtree)和“右子树”(right subtree) ,左子树和右子树是有顺序的
二叉树的常见概念
- 真二叉树: 不含一度节点的二叉树称作真二叉树(proper binary tree)
- 满二叉树:满二叉树也是真二叉树,且所有的叶子节点都在最后一层
- 完全二叉树: 深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
三.二叉搜索树
1.什么是二叉搜索树?
一般情况下存储数据我们可以采用数组的方式,但是从数组中检索数据的时间复杂度是O(n),如果数据存储有序,则可以采用二分查找的方式来检索数据,复杂度为:O(logn),但是如果操作数组中的数据像增加、删除默认数组会产生塌陷。时间复杂度为O(n)
二叉搜索树中查询、增加、删除复杂度最坏为O(logn),特性是当它的左子树不空,则左子树上所有结点的值均小于它的根结点的值,当右子树不空,则右子树上所有结点的值均大于它的根结点的值。
也称为:二叉查找树或二叉排序树
2.二叉搜索树的主要操作
二叉搜索树中的数据必须具有可比较性
- add 添加元素
- remove 删除元素
- size 元素个数
- contains 包含元素
树是没有索引的,不能通过索引来检索数据
3.实现二叉搜索树
class Node {
constructor(element, parent) {
this.element = element;
this.parent = parent;
this.left = null;
this.right = null;
}
}
class BST {
constructor() {
this.root = null;
this.size = 0;
}
add(element) {
if (this.root == null) {
this.root = new Node(element, null);
this.size++;
return;
}
let currentNode = this.root; // 默认从根节点开始查找
let parent = null;
let compare = null;
while (currentNode) {
compare = element - currentNode.element;
parent = currentNode; // 记住父节点
if (compare > 0) { // 大于当前节点放到右边
currentNode = currentNode.right;
} else if (compare < 0) {
currentNode = currentNode.left;
} else {
currentNode.element = element;
return;
}
}
let newNode = new Node(element, parent);
if (compare > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
this.size++;
}
}
let bst = new BST();
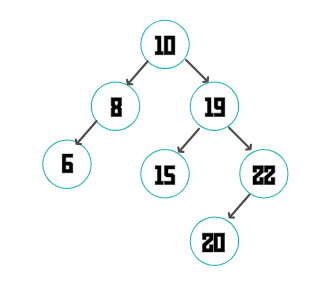
let arr = [10,8,19,6,15,22];
arr.forEach(item => {
bst.add(item);
});
console.dir(bst.root);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
4.复杂数据的存储
class Node {
constructor(element, parent) {
this.element = element;
this.parent = parent;
this.left = null;
this.right = null;
}
}
class BST {
constructor(compare) {
this.root = null;
this.size = 0;
this.compare = compare || this.compare;
}
compare(e1,e2){
return e1 - e2;
}
add(element) {
// ....
while (currentNode) {
compare = this.compare(element,currentNode.element);
// ....
}
// ....
this.size++;
}
}
let bst = new BST((e1, e2) => {
return e1.age - e2.age;
});
let arr = [{ age: 10 }, { age: 8 }, { age: 19 }, { age: 6 }, { age: 15 }, { age: 22 }];
arr.forEach(item => {
bst.add(item);
});
console.dir(bst.root);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
我们可以自定义比较器传递给二叉搜索树,内部调用比较器进行比较,从而存储数据
四.二叉树的遍历
线性数据结构遍历比较简单可以采用正序遍历、逆序遍历
1.二叉树的遍历方式
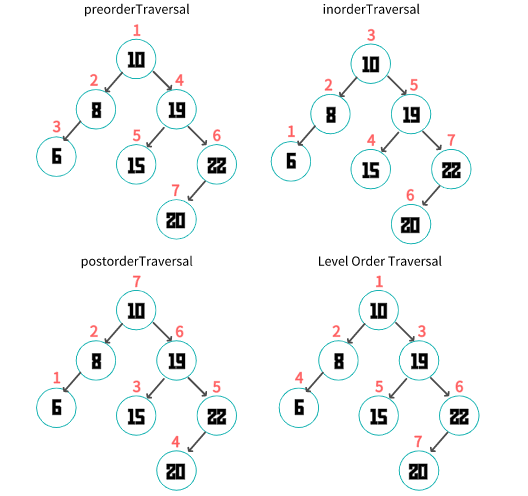
常见的二叉树遍历的四种方式
前序遍历
Preorder Traversal(先访问根节点、前序遍历左子树、前序遍历右子树)中序遍历
Inorder Traversal(中序遍历左子树、根节点、中序遍历右子树)后续遍历
Postorder Traversal(后序遍历左子树、后续遍历右子树、根节点)层序遍历
Level Order Traversal(从上到下,从左到右依次访问每一个节点)
2.前序遍历
preorderTraversal() {
const traversal = (node) => {
if (node === null) return
console.log(node.element); // 先访问根节点
traversal(node.left); // 在访问左子树
traversal(node.right);// 在访问右子树
}
traversal(this.root);
}
2
3
4
5
6
7
8
9
3.中序遍历
inorderTraversal() {
const traversal = (node) => {
if (node === null) return
traversal(node.left);
console.log(node.element);
traversal(node.right);
}
traversal(this.root);
}
2
3
4
5
6
7
8
9
对于二叉搜索树来说,中序遍历默认从小到大或者从大到小。
4.后续遍历
postorderTraversal() {
const traversal = (node) => {
if (node === null) return
traversal(node.left);
traversal(node.right);
console.log(node.element);
}
traversal(this.root);
}
2
3
4
5
6
7
8
9
5.层序遍历
levelOrderTraversal() {
if (this.root == null) return;
let stack = [this.root];
let currentNode = null;
let index = 0;
while (currentNode = stack[index++]) {
console.log(currentNode.element);
if (currentNode.left) {
stack.push(currentNode.left);
}
if (currentNode.right) {
stack.push(currentNode.right);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
五.遍历树对节点进行操作
通过访问器模式获取节点,对节点进行操作处理
preorderTraversal(visitor) {
if(visitor == null) return;
const traversal = (node) => {
if (node === null) return
visitor.visit(node.element);
traversal(node.left);
traversal(node.right);
}
traversal(this.root);
}
inorderTraversal(visitor) {
if(visitor == null) return;
const traversal = (node) => {
if (node === null) return
traversal(node.left);
visitor.visit(node.element);
traversal(node.right);
}
traversal(this.root);
}
postorderTraversal(visitor) {
if(visitor == null) return;
const traversal = (node) => {
if (node === null) return;
traversal(node.left);
traversal(node.right);
visitor.visit(node.element);
}
traversal(this.root);
}
levelOrderTraversal(visitor) {
if (this.root == null || visitor == null) return;
let stack = [this.root];
let currentNode = null;
let index = 0;
while (currentNode = stack[index++]) {
visitor.visit(currentNode.element)
if (currentNode.left) {
stack.push(currentNode.left);
}
if (currentNode.right) {
stack.push(currentNode.right);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
通过调用传入的
visit方法可以将遍历到的结果传入到visit函数中。用户可以自行处理每次遍历到的结果。
六.翻转二叉树
invertTree(){
if (this.root == null) return;
let stack = [this.root];
let currentNode = null;
let index = 0;
while (currentNode = stack[index++]) {
let tmp = currentNode.left;
currentNode.left = currentNode.right;
currentNode.right = tmp
if (currentNode.left) {
stack.push(currentNode.left);
}
if (currentNode.right) {
stack.push(currentNode.right);
}
}
return this.root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
翻转二叉树的核心就是树的遍历+左右节点互换而已
七.前驱节点 & 后继节点
对一棵二叉树进行中序遍历,遍历后的顺序,当前节点的前一个节点为该节点的前驱节点;
predesessor(node) {
if (node == null) return null;
let prev = node.left;
if (prev !== null) { // 找左子树中最右边的节点
while (prev.right !== null) {
prev = prev.right;
}
return prev;
}
// 当前父节点存在,并且你是父节点的左子树
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
return node.parent;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
对一棵二叉树进行中序遍历,遍历后的顺序,当前节点的下一个节点为该节点的后继节点;
successor(node) {
if (node == null) return null;
let next = node.right;
if (next !== null) { // 找左子树中最右边的节点
while (next.left !== null) {
next = next.left;
}
return next;
}
// 当前父节点存在,并且你是父节点的左子树
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
return node.parent;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
八.删除节点
remove(element) {
let node = this.node(element);
if(node == null) return;
this.size--;
// 度为2的节点
if(node.left !== null && node.right !== null){
let pre = this.successor(node);
node.element = pre.element;
node = pre;
}
// 度为1的节点
let replace = node.left || node.right;
if(replace !== null){
replace.parent = node.parent;
if(node.parent == null){
this.root = replace;
}else if(node == node.parent.left){
node.parent.left = replace;
}else{
node.parent.right = replace;
}
// 根节点
}else if(node.parent == null){
this.root = null;
// 叶子节点
}else{
if(node == node.parent.left){
node.parent.left = null;
}else{
node.parent.right = null;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33